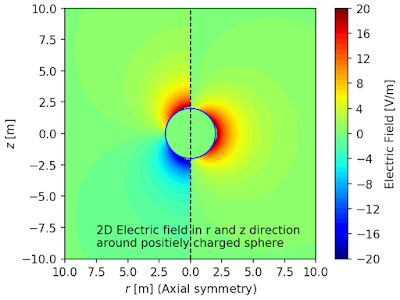
The result is:

This page shows how to combine two contourf and one colorbar into one figure using python and matplotlib.pyplot. The example is the axial symmetric model which has r-z coordinates. The z axis is the axis of symmetry. A charged sphere is placed at (r,z)=(0,0) and electric field distribution around the sphere is calculated and plotted into a figure. The right side of the figure is electric potential in r direction, and the left side is electric field in z direction.

See also:

Python Matplotlib Tips: Combine two contourf and two colorbar into one figure using Python and matplotlib.pyplot

This page shows how to combine two contourf and two colorbar into one figure using python and matplotlib.pyplot.

In [1]:

import matplotlib.pyplot as plt
import numpy as np

Define constants

In [2]:

eps0 = 8.85*10**(-12) # permittivity of vacuum
rho_sp = 2.0          # radius of the sphere
Q_sp = 1.0*10**(-8)   # charge of the sphere

Generate two data (Er: Electric field in r direction and Ez: Electric field in z direction) to show in one figure.

In [3]:

Ndata = 1000
rs = np.linspace(10**(-12),10,Ndata)
zs = np.linspace(-10,10,Ndata)
RR,ZZ = np.meshgrid(rs,zs)

def funcErz(rsp,q,x,y):
    rho = (x**2+y**2)**0.5
    e = q/(4*np.pi*eps0*(x**2+y**2))
    esp = 0
    e[np.where(rho<rsp)] = esp
    er = e*x/rho
    ez = e*y/rho
    return er,ez
    
Er,Ez = funcErz(rho_sp, Q_sp, RR, ZZ)

Convert the data to figure

In [4]:

fig = plt.figure(facecolor='w')
ax = fig.add_subplot(1, 1, 1)
ax.set_aspect('equal')

cmin = -20
cmax = 20
lvls = np.linspace(cmin, cmax, 50)

# Right side of the figure which shows V: electric potential
cont1 = ax.contourf(RR, ZZ, Er, levels=lvls, cmap='jet')
# Left side of the figure which shows E: electric field
cont2 = ax.contourf(-RR, ZZ, Ez, levels=lvls, cmap='jet')

# Plot one colorbar at the right side of the figure
cbar = plt.colorbar(cont1)
cbar.set_label('Electric Field [V/m]')
cbar.set_ticks([np.arange(cmin, cmax+0.001,4)])
# cbar.set_ticklabels([ "$10^{%d}$"%(int(x)) for x in cbar1.get_ticks()])

# Additional data 1: a line to separate left side and right side
ax.plot([0,0], [-10,10], 'k--', lw=1)

# Additional data 2: shape of the spere
tsp = np.linspace(0, 2*np.pi, 100)
xsp = rho_sp*np.cos(tsp)
ysp = rho_sp*np.sin(tsp)
ax.plot(xsp,ysp,'b-',lw=1)

# Additional data 3: text
tx =  "2D Electric field in r and z direction "+"\n"
tx += "around positiely charged sphere"
ax.text(-7.5, -9, tx)

# Set ticks and labels
xtks = ax.get_xticks()
ax.set_xticks(xtks)
ax.set_xticklabels(np.abs(xtks))
ax.set_xlabel('$r$ [m] (Axial symmetry)')
ax.set_ylabel('$z$ [m]')

# Save figure as png file
plt.savefig("two_contour_one_colorbar_in_one_figure.png",
            bbox_inches='tight', pad_inches=0.05, dpi=150)
plt.show()

Combine two contourf and one colorbar into one figure using Python and matplotlib.pyplot